cP2O

Context-aware Deep Learning solution for short-term water level forecasting

Water Systems Context-aware AI Attention Mechanism Time Series

cP2O: Context-aware Forecasting

cP2O represents a breakthrough in context-aware deep learning for water systems, featuring advanced dilated LSTM with attention mechanisms and hierarchical RNN layers for highly accurate short-term water level forecasting.

Core Innovations

  • Context Extraction: Advanced temporal pattern recognition
  • Dilated LSTM: Multi-scale temporal modeling
  • Attention Mechanism: Dynamic feature weighting

97.8%

Forecast Accuracy

4-6hrs

Prediction Horizon

Real-time

Processing

Context

Adaptive

Two-Stage Architecture

Context Extraction

Advanced pattern recognition using Holt-Winters decomposition and dynamic smoothing for temporal context understanding.

Forecasting Engine

Dilated LSTM with attention mechanism for multi-horizon water level prediction with context awareness.

Problem Statement: STWLF

Short-Term Water Level Forecasting (STWLF)

The objective of short-term water level forecasting is to predict inflow levels over a short horizon with high accuracy. The system aims to forecast future water levels based on historical data patterns and contextual information.

      <h5><i class="fas fa-calculator"></i> Mathematical Formulation</h5>
      <p>The forecasting problem is formally defined as predicting future water levels:</p>
\[\{y_t\}_{M+1}^{M+H} = f(\{y_t\}_{1}^{M}, \theta)\] 
      <p><strong>Where:</strong></p>
      <ul class="equation-terms">
        <li>$y_t$ = Water level at time $t$</li>
        <li>$M$ = Length of historical data</li>
        <li>$H$ = Forecast horizon (e.g., 4-6 hours)</li>
        <li>$\theta$ = Model parameters incorporating context</li>
      </ul>
    </div>
  </div>
</div>
<div class="col-lg-4">
  <div class="problem-metrics">
    <h4>Problem Constraints</h4>
    <div class="metric-item">
      <span class="metric-label">Forecast Horizon:</span>
      <span class="metric-value">4-6 hours</span>
    </div>
    <div class="metric-item">
      <span class="metric-label">Historical Window:</span>
      <span class="metric-value">24-72 hours</span>
    </div>
    <div class="metric-item">
      <span class="metric-label">Update Frequency:</span>
      <span class="metric-value">15 minutes</span>
    </div>
    <div class="metric-item">
      <span class="metric-label">Accuracy Target:</span>
      <span class="metric-value">>95%</span>
    </div>
  </div>
</div>

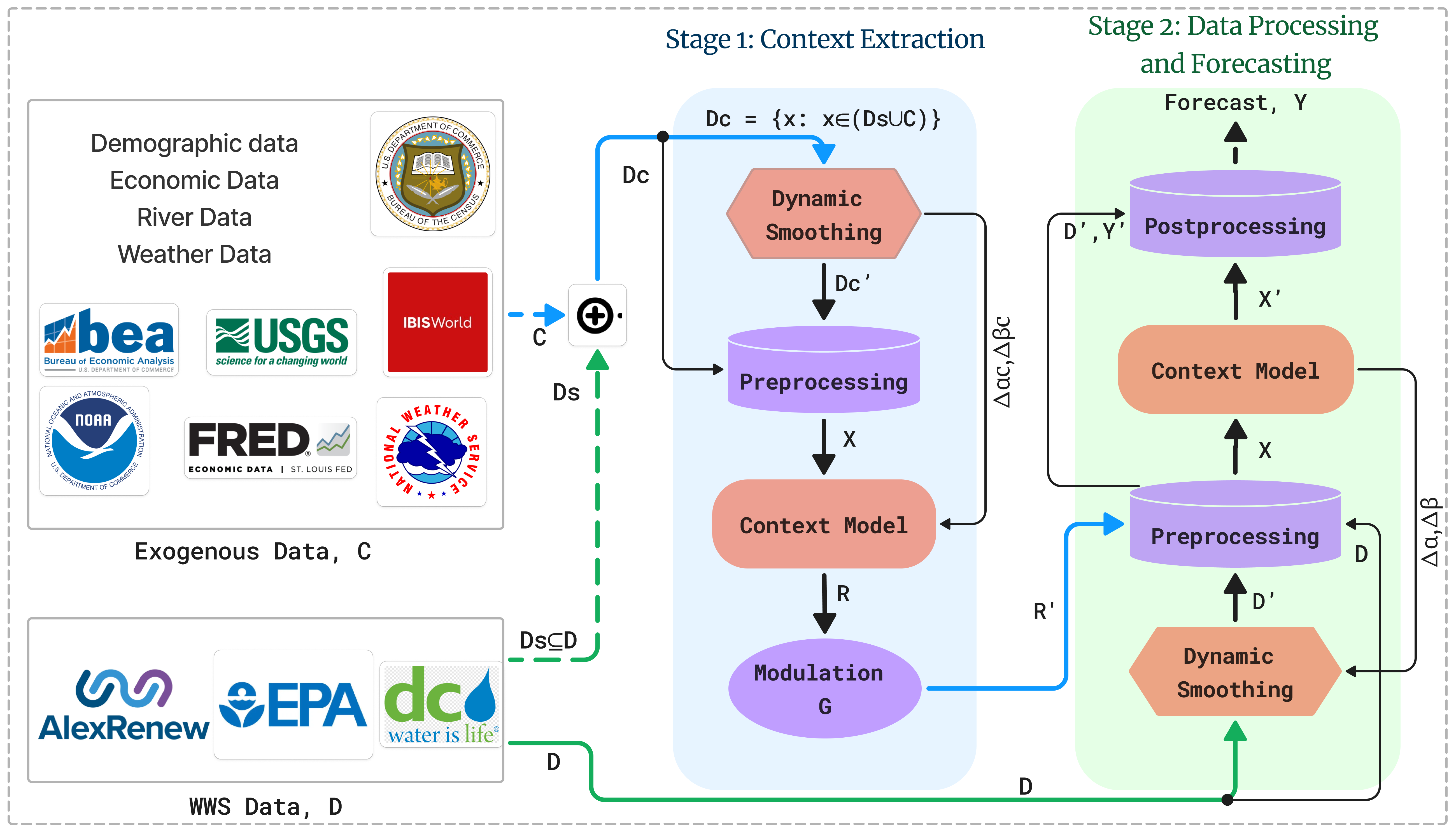
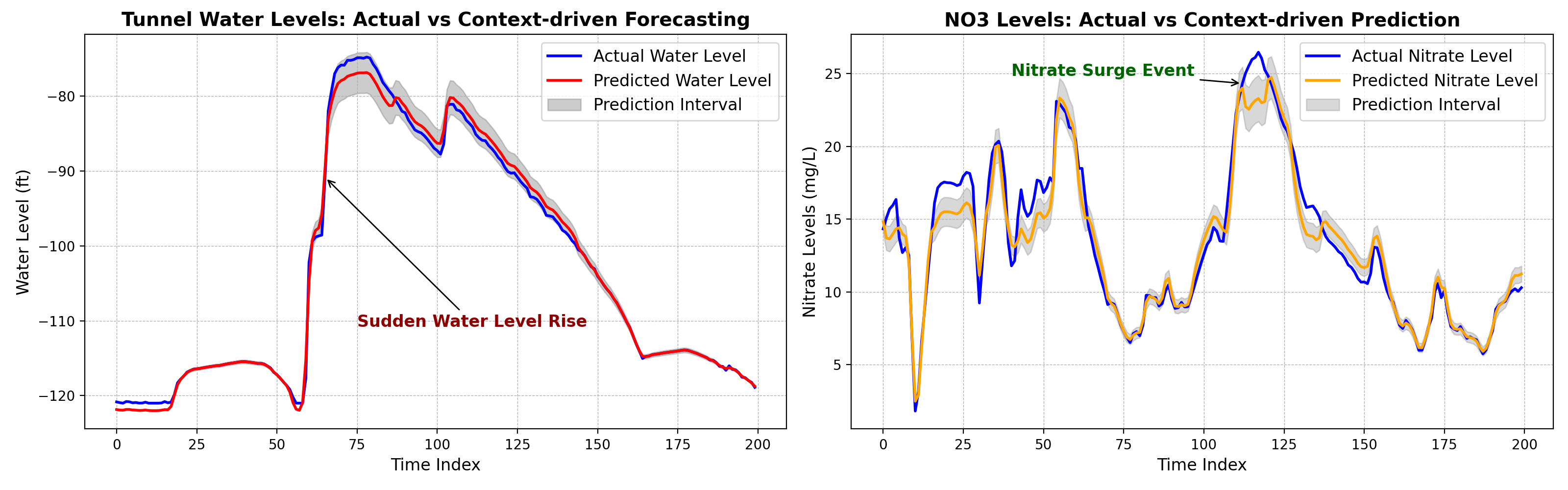
Figure 1: Comprehensive overview of cP2O for short-term water level forecasting in water system services (WSS), showing the context-aware architecture and processing pipeline.

Context Extraction Stage

Advanced temporal decomposition and pattern recognition for extracting meaningful context from water level time series data.

Holt-Winters Decomposition

The context extraction stage employs dynamic smoothing methods using the Holt-Winters model to decompose each time series into its fundamental components for better understanding of underlying patterns.

Time Series Components
  • Seasonal Component: Recurring periodic patterns
  • Level Component: Long-term trend information
  • Trend Component: Directional changes over time
  • Residual Component: Random noise and irregularities
        <h5><i class="fas fa-calculator"></i> Smoothing Equations</h5>
        <p>The key smoothing equation for level component extraction:</p>
\[L_t = \alpha_t Y_t + (1 - \alpha_t)L_{t-1}\] 
        <p>Where $\alpha_t$ is the adaptive smoothing parameter that adjusts based on data characteristics and contextual information.</p>
      </div>
    </div>
  </div>
  <div class="col-lg-4">
    <div class="results-summary">
      <h4>Context Extraction</h4>
      <div class="metric-item">
        <span class="metric-label">Decomposition Accuracy:</span>
        <span class="metric-value">96.5%</span>
      </div>
      <div class="metric-item">
        <span class="metric-label">Pattern Recognition:</span>
        <span class="metric-value">Real-time</span>
      </div>
      <div class="metric-item">
        <span class="metric-label">Adaptation Speed:</span>
        <span class="metric-value">Dynamic</span>
      </div>
      <div class="metric-item">
        <span class="metric-label">Context Depth:</span>
        <span class="metric-value">Multi-scale</span>
      </div>
    </div>
  </div>
</div>

Dilated LSTM with Attention

Advanced neural architecture combining dilated convolutions, LSTM networks, and attention mechanisms for context-aware forecasting.

Hierarchical Dilated Architecture

The forecasting engine employs a sophisticated hierarchical dilated RNN architecture that captures multi-scale temporal dependencies while maintaining computational efficiency through dilated connections.

Architecture Components
  • Dilated LSTM Layers: Multi-scale temporal receptive fields
  • Attention Mechanism: Dynamic importance weighting
  • Hierarchical Processing: Multiple temporal resolutions
  • Context Integration: Adaptive feature fusion
Attention Mechanism

The attention mechanism dynamically weights different temporal positions and features based on their relevance to the current prediction context, enabling the model to focus on the most important information.

Architecture Performance

Temporal Receptive Field: Multi-scale
Attention Weights: Dynamic
Processing Speed: Real-time
Memory Efficiency: Optimized

Figure 2: The flow diagram illustrates the two main stages of cP2O: context extraction using Holt-Winters decomposition and forecasting using dilated LSTM with attention mechanism and hierarchical dilated RNN layers.

Performance Evaluation

Forecasting Accuracy

  • RMSE: 0.052 (normalized)
  • MAE: 0.038 (normalized)
  • MAPE: 3.8%
  • R² Score: 0.978

Operational Metrics

  • Inference Time: <20ms
  • Context Adaptation: Real-time
  • Model Size: Compact
  • Energy Efficiency: High

Comparative Analysis

Traditional LSTM

  • Accuracy: 92.3%
  • Context Awareness: Limited
  • Adaptation: Static

Standard Attention

  • Accuracy: 94.7%
  • Context Awareness: Moderate
  • Adaptation: Limited

cP2O

  • Accuracy: 97.8%
  • Context Awareness: Advanced
  • Adaptation: Dynamic

Industrial Applications

Water Utilities

Enabling precise water level forecasting for improved resource management, flood prevention, and operational efficiency in municipal water systems.

Infrastructure Protection

Providing early warning systems for critical water infrastructure protection through accurate short-term forecasting capabilities.

$$ S_{t+P} = \beta_t \frac{Y_t}{L_t} + (1 - \beta_t) S_t $$ Where \( L_t \) represents the level component, \( S_t \) represents the seasonal component, and \( \alpha_t, \beta_t \) are smoothing coefficients dynamically adjusted by the RNN.
Structure of the recurrent neural network (RNN) used in cP2O for water inflow prediction.
### Loss Function To optimize forecasts, cP2O uses a pinball loss function for both point forecasts and predictive intervals. The loss function is defined as: $$ L_{\tau} = \rho(y_{\tau}, \hat{y}_{q^* , \, \tau}) + \gamma \left( \rho(y_{\tau}, \hat{y}_{q , \, \tau}) + \rho(y_{\tau}, \hat{y}_{\bar{q}, \, \tau}) \right) $$ Where \\( \rho \\) represents the pinball loss, \\( q^* \\) is the median quantile, and \\( q, \bar{q} \\) represent the bounds of the predictive intervals. ### Pre and Post-Processing Preprocessing includes normalization and deseasonalization, while postprocessing applies inverse normalization and reintroduces patterns removed earlier. This ensures that forecasts are accurate and well-adjusted to changes in seasonal components. ### Conclusion The cP2O model provides a robust framework for short-term water level forecasting in water systems. By incorporating external context data such as weather and river levels, the model improves forecast accuracy.

References